다면체에서의 오일러 표수, V - E + F = 2 증명 Proof of Euler's characteristic in polyhedron

오일러 표수라는 말이 낯설게 느껴질 수 있는데,

중학교 때 배웠던 다면체에서의 공식이다.

V-E+F=2 말이다.

기존 동영상에서 설명을 했던 것인데,

이 자료에 대한 사진으로 설명 및 증명을 하겠다.

V : 꼭지점의 수 E : 모서리의 수 F : 면의 수

평면으로 이루어진 다면체에서는 V-E+F=2 가 성립한다.

그림에 설명이 있으니, 보고 이해하면 되겠다.

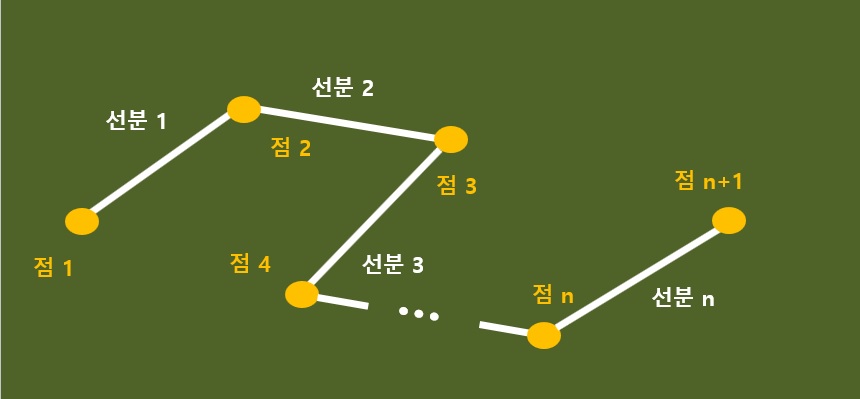
꺾은 선을 보면 선과 점의 갯수 차이가 1개이다.

점과 선분을 차례대로 표시해보면 나오는 결과이다.

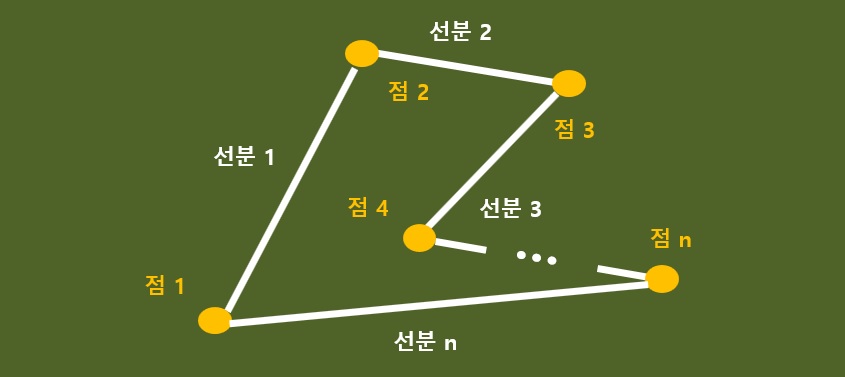
위 선을 링(ring) 처럼 만들면 갯수 차이가 없다.

이것도 위와 마찬가지로 점과 선에 번호를 매겨보면서 해보라.

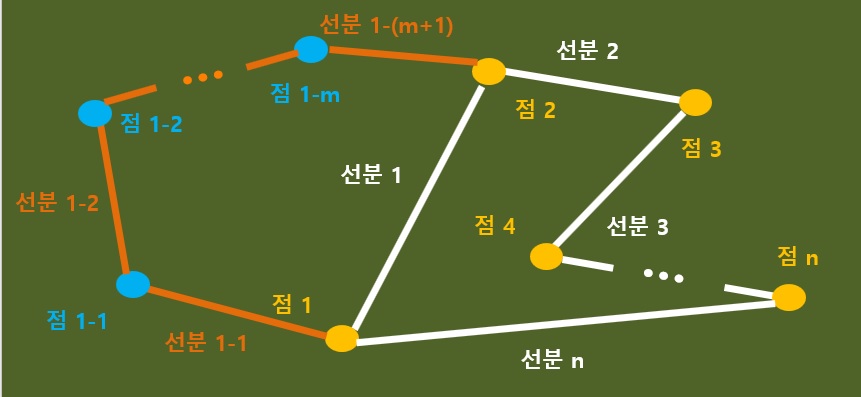
옆에 선을 더 그려서 면을 하나 더 만들어 보자.

이것도 똑같이 다른 방식으로 번호를 매겨서 확인 해봐라.

이 때 오일러 표수를 알아보자. 오일러 표수의 이전과 차이가 없다.

갯수를 문자로 나타냈는데,

첫 번째로 나온 링(ring) 그림의 점,선, 면의 수를 노란색으로 표시했고,

추가된 링의 것의 수를 빨간색으로 표시했다.

결과는 그림을 보면 설명이 잘 되어있다.

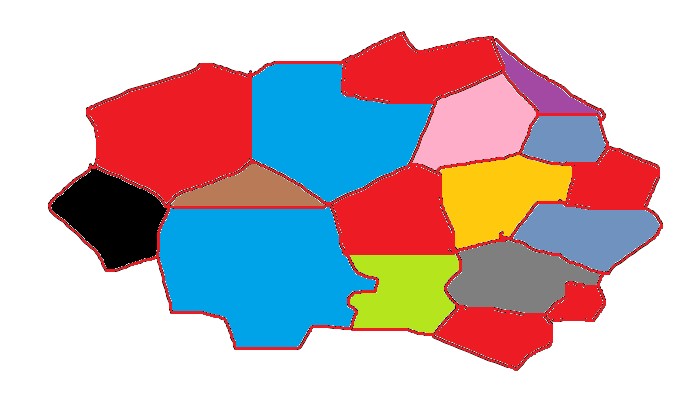
면을 덕지덕지 붙이면 이런 식으로 될 것이다.

그림판으로 추하게 그렸는데,

컨셉이 이렇다라는 것이다.

저런 면을 점과 선, 면의 갯수 변화 없이 저런 바구니 형태로 만들 수 있다.

갯수 변화 없이 선을 늘렸다 줄였다 하면된다.

갯수를 파악하는 거니까 모양은 변해도 관계없다.

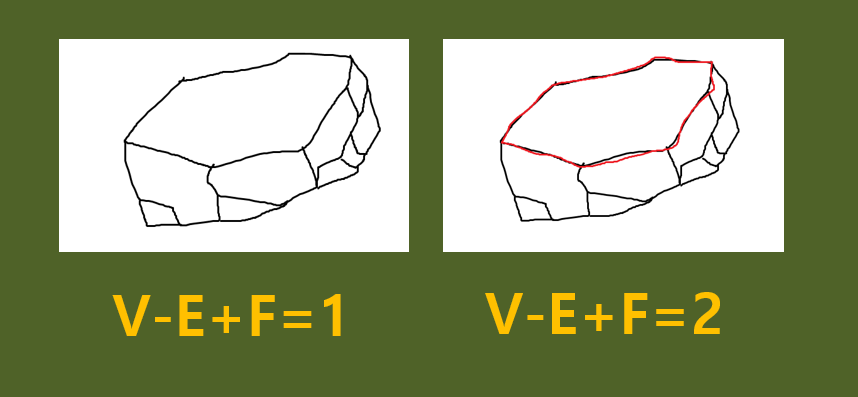
바구니에 뚜껑을 얹어놓으면 오일러 표수가 1에서 2가 된다.

뚜껑을 얹으니, 면이 하나 더 생기니까 F의 수가 하나 더 늘어나니까

표수도 당연히 하나 더 늘어나는 것이다.

보충해서 듣고 싶으면 아래 영상을 참고하면 되겠다.

대스마