왜 정다면체는 5개 뿐인가? Why does the world have only 5 platinic solids?

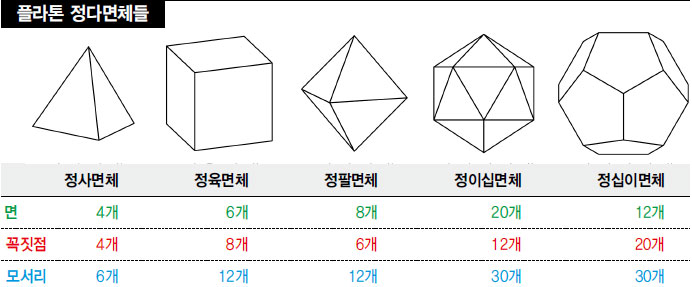
세상엔 다면체가 많지만

정다면체라 할만한 건 5개 뿐이다.

다면체의 모든 면이 정다각형으로

똑같다는 조건이 있기 때문이다.

이번 글에서는 왜 5개 밖에 없는지를 알아보겠다.

순서는 위 세 가지 부터 파악하고

다면체에 우리가 본격적으로 알고자하는 주제에 대해 얘기하도록 하겠다.

직선이 하나 있다고 해보자.

여기서 이 직선과 일치하지 않고 

평행하지 않은 선을 하나 더 그을 수 있다.

하나 더 그으면 필연적으로 두 선이 만나서 점이 생기게 된다.

이 상태에서 직선을 하나 더 긋는데,

기존에 생긴 점을 지나지 않고,

두 직선과 일치하거나 평행하지 않는 직선을 하나 더 긋도록 하겠다.

그러면 점 2개가 더 생기고 면이 하나 생기게 된다.

점과 각이 3개가 되고 삼각형이라 불리는 면이 생기는데,

여기서 알 수 있는 사실은

면이 하나 생기는데 필요한 최소 선분과 점의 갯수가 3개라는 점이다.

직선에 대해 파악하고, 면이라는 존재를 알아냈으니,

평면에 대해 알아보도록 하자.

직선에 대해 파악해본 방식과 동일하게

이 평면과 평행하지 않고 일치하지 않은 평면을 하나 더 그려보자.

그려보니 직선이 하나 더 생기게 되었다.

여기서 두 평면과 일치하지 않고, 평행하지도 않은 평면을 하나 더 추가해보자.

그러면 직선 하나가 더 생기고, 점이 생기게 되었다.

평면이 적어도 3개는 있어야 점이 하나가 생긴다는 사실을 알아냈다.

이 사실은 뒤에 설명할 각뿔과 연관되어 있으니,

기억하기 바란다.

이번엔 각도와 길이에 대해 알아볼 것이다.

각도라는 게 뭔가?

두 직선이나 선분이 벌어진 정도를 얘기하지 않는가?

어떤 걸 기준으로 해서 재느냐에 따라 다른데,

빨간 부분을 예각, 파란 부분을 둔각이라고 한다.

여기에선 두 각의 크기가 다르므로

이런 식으로 구분 할 수 있다.

두 각이 같은 경우에는 직각이라고 한다.

그렇다면 앞에 설명했던 둔각과 예각을 설명할 기준 각이 생긴다.

직각보다 작은 각은 예각,

크면 둔각이라고 할 수 있다.

직각일 때 이 각의 크기를 R이라고 하면,

( 영어로 직각이 Rectangle이고, 여기서 R을 따서 썼다. )

원 반바퀴는 빨간색 파란색 합친 것이고,

두 각이 같으니,

R+R=2R 이 된다.

반 바퀴를 두개 합치면, 한 바퀴가 되니,

2R+2R=4R 이 된다.

원 한 바퀴는 각도가 직각 4개와 같다.

앞에 말했던 둔각과 예각이 있는데,

빨간 거 파란 거 두 개 합치면 직각 2개와 같다는 걸 알 수 있을 것이다.

여기서 더 나아가면 그림에서 보이는 파란 것들과 빨간 것들이 있는데,

색이 같은 것들은 같은 각도라는 사실을 알 수 있다.

파란색 부분과 빨간색 부분을 합쳐서 직각 2개와 같을 때,

(직각 하나를 90도라 했을 때, 직각 2개는 180도이다.)

이 때 흰 색 두 직선을 평행이라고 하는데,

빨간 부분을 동위각 관계,

파란 부분을 엇각 관계라고 할 수 있다.

같은 색을 가진 각들이 서로 같음을 알 수 있다.

흰 색 두 선은 서로 평행한 직선이고,

주황색 선과 남색선은 그림과 같이

 흰 색 선에 위 한 점에서 만나고,

서로 일치하지 않게 선을 그으면

위의 그림과 같이 되고,

선들이 만들어낸 닫힌 공간은

삼각형이 된다.

여기서 삼각형의 각이 있는데,

노란색 각과 빨간색 각의 엇각을 찾아내면,

그림과 같이 되는데,

합치면 180도가 되는 것을 알 수 있다.

삼각형이 있을 때,

각을 하나 더 만드려고 하면,

위의 그림과 같이 될 것인데,

전체 그림은 사각형이 된다.

그림을 보면 알겠지만,

사각형은 삼각형 2개를 놓은 것과 같은 그림이 된다.

그렇다면 사각형의 각은 어떻게 되겠는가?

삼각형 각의 두 배가 된다는 걸 알 수 있다.

즉, 360도가 된다.

다각형에서 각이 하나씩 추가되면서

삼각형이 하나씩 추가되는 그림이 보임을 알 수 있다.

이런 패턴을 표로 보면 아래와 같다.

임의의 다각형 n각형은

삼각형이 n-2 개가 있다고 할 수 있다.

이번엔 거리에 대해 생각하면,

원의 중심과 직선과의 거리를 보면,

주황색이 원의 반지름보다 짧고,

흰색은 원의 반지름 길이며,

파란색이 원의 반지름 보다 길다.

이 세 선이 원과 만나는 모습을 보면,

주황색은 2 점

흰색은 1 점

파란색은 만나지 않는다.

원과 두 점에서 만나는 경우를 보면,

그림에서 보는 것과 같이,

원 안의 선분의 길이는 원의 반지름과 같다.

따라서, 저 위에 있는 삼각형은 이등변 삼각형이다.

저 밑변을 반으로 갈라보도록 하자.

그러면, 갈라진 두 삼각형은 서로 합동임을 위의 그림을 보고 알 수 있다.

선분 AB를 반으로 가른 선을 기준으로 양쪽 각은 직각임을 알 수 있다.

직선은 각도로 따지면 원 반바퀴라 180도 이기 때문이다.

 그림의 초록색 각이 줄어든다면, 

붉은색 각이 늘어날 것이다.

삼각형의 내각의 합은 180도로 일정하고,

노란색 부분은 90도이기 때문에

초록부분 붉은부분의 합은 일정하기 때문이다.

초록색이 계속 줄어들어 각이 0도가 되면,

붉은 부분은 90도가 될 것이다.

이런 식으로 말이다.

선이 원에 접하고, 선과 원 중심 거리는 원의 반지름,

위의 선분끼리는 서로 수직이라는 걸 알 수 있다.

원 중심에서 다른 곳으로 선을 그어보면,

위의 그림과 같이 나타나는데,

원 밖의 점이므로,

원의 반지름보다 길다는 걸 알 수 있다.

점 H로부터 멀리 선을 그을수록,

각이 작아짐을 알 수 있는데,

노란색과 파란색 부분을 보면 알 수 있다.

붉은 부분의 각은 직각이다.

이로써 직각삼각형에서 높이가 같을 때,

밑변의 길이가 길수록 밑변과 빗변이 이루는 각이 작아짐을 알 수 있다.

이제 각뿔과 다면체 이야기다.

여기에 다면체 하나가 있다고 하자.

한 점으로 모인곳이 하나 보일 것이다.

이런 도형을 각뿔이라고 한다.

각뿔 유형의 다면체는 다면체에서 

한 꼭지점 근처를 잘라내면 나오는 부분이라고 볼 수 있다.

각뿔부분에서 아까 설명했던 부분과 같이 생각해보자.

각뿔은 면이 한 점으로 모이는 부분이 있는 도형이라했다.

면이 한 점을 만드려면 적어도 3개가 있어야 한다고 했다.

그러면 위 꼭지점에 모인 면이 3개 이상 되어야 한다는 뜻이 된다.

이 각뿔의 꼭지점에서 밑면으로 수선을 내리고,

수선의 발을 중심으로 각 점에 연결하면,

오른쪽 그림과 같이 될 것이다.

여기서 빨간색으로 동그라미 친 부분을 보도록 하자.

선분 OH는 위의 평면과 수직한 선이므로,

선분 AB와 수직이라 할 수 있다.

그리고 선분 OI를 선분 AB의 수선을 긋고,

선분 HI를 그어보자.

그러면 선분 OI와 선분 HI를 비교했을 때,

선분 HI가 더 짧다는 걸 알 수 있다.

좀 전에 언급했던 부분을 기억해서

위 그림과 같이 유추할 수 있고,

이런 결과를 도출해낼 수 있다.

나아가 이런 사실을 보일 수 있으며,

수선의 발에 모인 부분을 합치면,

원 한바퀴가 되니 360도이고,

각뿔의 꼭지점에 모인 각들의 합은

360도 보다 작아야 함을 알 수 있다.

여기까지에서 결론은 아래와 같이 낼 수 있다.

1. 입체도형이 되려면 가져야하는 면의 수에 관한 조건

2. 꼭지점에 모이는 각에 대한 조건

두 가지로 입체도형을 설명할 수 있을 것이다.

그림에 설명이 나와있으니 읽어보면 되겠다.

정n각형은 내각의 합이 180(n-2) 도이다.

따라서 한 내각의 크기는 위 그림과 같다.

각 정다각형에 대입하면

위 그림과 같다.

정삼각형에서 정육각형까지 구해놓은 것이다.

여기서 입체도형의 조건 1을 보면,

꼭지점에 모이는 면의 수는 3개 이상이어야 하고,

조건 2는 이 각의 합이 360도 보다 작아야 한다.

즉, 하나에 120도 보다 작아야 하므로,

정다면체의 면에 정육각형은 탈락이고,

정삼각형, 정사각형, 정오각형만 된다는 것을 알 수 있다.

이렇다면, 두 조건에 의해

정삼각형, 정사각형, 정오각형은 몇 개까지 

한 꼭지점에 모이는 게 가능한지 보면,

정삼각형은 3, 4, 5 개

정사각형, 정오각형은 3개 가능하다.

결국 정다각형은 5개 뿐이라는게 밝혀졌다.

이제 정다면체에는 어떤게 있는지 알아보자.

정n면체은 정m각형으로 둘러싸인 도형이라고 해보자.

정m각형이 n개가 있을 건데,

각 도형별로 각자 꼭지점과 선분의 수를 세어보면

nxm=nm 개가 될 것이다.

정n면체에서 한 꼭지점에 모인 갯수를 k개라고 하면,

정다면체면 한 꼭지점에 모인 갯수도 같으므로,

꼭지점은 각자 셀 때 합에서 k를 나눠야 한다.

각자 셀 때는 꼭지점을 k번 중복해서 센 것과 같기 때문이다.

그러면 정n면체에서의 꼭지점 갯수는 nm/k 개이다.

선분은 두 면이 만났을 때 생기는 것이므로,

각 정m각형을 셀 때는 선분을 2번 중복해서 센 것과 같다.

그래서 각자 셌을 때에 2를 나눠줘야 한다.

따라서 정n면체의 모서리 갯수는 nm/2 개이다.

정리하면 꼭지점, 면, 모서리 수는 위의 그림과 같다.

여기에 오일러 표수와 연관시키면,

식은 주황색 글과 같이된다.

위 식을 n으로 묶어서 이항시키면,

그림 가장 아래의 식으로 n을 구할 수 있다.

정n면체에 n을 구할 수 있다는 얘기다.

정리하면, 그림과 같다.

정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체

이렇게 5개가 나온다.

이 내용을 듣고 싶은 사람은 아래 영상을 참고하면 된다.